Bobblemaze je typ číselného rébusu, ve kterém se za pomoci logických úvah hledá cesta v bludišti. Jeho autorem je Jiří Poláček z Ekonomicko-správní fakulty Masarykovy univerzity. Jeho inspirací byla matematická hříčka publikovaná v knize rekreační matematiky, kořeny vzniku rébusu však sahají až do doby před téměř třiceti lety. Postup řešení rébusu z dubnového čísla muni.cz a různé autorovy tipy k vyřešení najdete v textu níže. Další rébus vyjde v květnovém čísle. Publikovaná řešení by měla mít právě jedno řešení.
Najděte posloupnost sousedních čísel začínající v čísle 1 a končící v čísle s nejvyšší hodnotou tak, aby v libovolném pořadí obsahovala (s výjimkou nuly) všechna čísla právě jednou. Nula nikdy není součástí řešení; čísla spolu sousedí, pokud mezi nimi není přepážka, pouze ve směrech nahoru-dolů, doleva-doprava, nikdy ne šikmo.
Obtížnost: velmi snadné
řešení rébusu z dubnového čísla muni.cz
UKÁZKY ŘEŠENÍ A TIPY
Bobblemaze je typ číselného rébusu, ve kterém se za pomoci logických úvah hledá cesta v bludišti. Vyřešené zadání může vypadat například jako na obr. 1.
Stručné zadání: Najděte posloupnost sousedních čísel začínající v čísle 1 a končící v čísle s nejvyšší hodnotou tak, aby v libovolném pořadí obsahovala (s výjimkou nuly) všechna čísla právě jednou. Nula nikdy není součástí řešení; čísla spolu sousedí, pokud mezi nimi není přepážka, pouze ve směrech nahoru-dolů, doleva-doprava, nikdy ne šikmo.
Tipy pro řešení rébusu
- Nula není součástí řešení.
- Číslo, které se mezi nevyřešenými čísly vyskytuje pouze jednou, musí být součástí řešení. Koncové prvky cesty jsou dány jednoznačně a mohou být pro lepší přehlednost vypsány tučně.
- Pokud má číslo, které je součástí řešení, pouze dva sousedy, musejí i tato sousední čísla být součástí řešení.
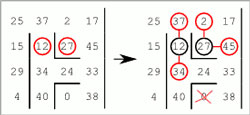
- Nevyřešené číslo, které má maximálně jednoho souseda, nemůže být součástí řešení.
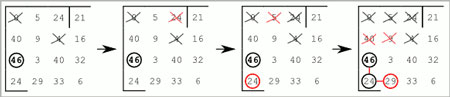
- Pokud se číslo, které je součástí řešení, nachází v oblasti, do které může řešená cesta vést vždy výhradně přes daná nevyřešená čísla, tak i tato čísla musejí být součástí řešení.
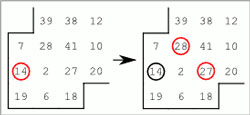
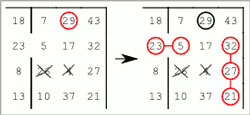
- Některá čísla lze vyřešit metodou sporu – vyslovíme-li hypotézu, že vybrané číslo je/není součástí řešení, můžeme aplikací navazujících logických úvah dojít ke sporné situaci, například že číslo, které je součástí řešení, lze spojit jenom s jedním sousedem či naopak by mělo být spojeno se třemi sousedy.
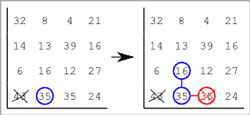
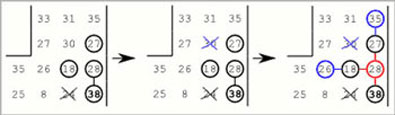
- Při uplatňování výše zmíněných pravidel je zapotřebí myslet na speciální případy, kterými jsou koncová čísla cesty – ta se spojují jenom s jedním sousedním číslem.
- Obecně lze vytvořit zadání, které bude mít více řešení. Publikovaná řešení by však měla mít právě jedno řešení.
